学习笔记——LORA微调
学习笔记——LORA微调
LORA是一种低资源微调LLM模型的方法,源自论文:LoRA: Low-Rank Adaptation of Large Language Models。
一、高效微调
对于语言模型来说,在微调过程中,模型加载预训练参数\(\Phi_{0}\)进行初始化,并通过最大化条件语言模型概率实现参数调整$_{0}+$,即: \[ max_\Phi\sum_{(x,y)\in\mathcal{Z})}\sum_{t=1}^{|y|}log(P_\Phi(y_t|x,y<t)) \] 这种方式的主要缺点参数增量\(\Delta\Phi\)的维度和预训练参数\(\Phi_{0}\)是相同的,所需资源比较多,一般被称为full fine-tuing。
为了用更少的参数来表示学习增量\(\Delta\Phi\),提出了一系列方法叫做高效微调。例如:Adapter、prefixtuning等。相比于其他方法LORA使用一个低秩矩阵来编码参数增量,这种方法不会增加推理耗时并且便于优化。
二、实现方式
研究表明:预训练模型拥有极小的内在维度(instrisic dimension,表示数据变化的自由变量的个数),换而言之,存在一个极低维度的参数,微调它和在全参数空间中微调能起到相同的效果。
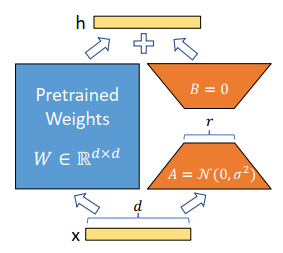
该论文认为参数矩阵更新的过程中也存在一个‘内在秩’。对于预训练的权重矩阵\(W_0\),可以用一个低秩分解来表示参数更新\(\Delta W\),即: \[ W_0+\Delta W=W_0+BA\quad B\in\mathbb{R}^{d\times r},A\in\mathbb{R}^{r\times k}\quad and\quad r\ll min(d,k) \] 训练过程中可以冻结参数\(W_0\),只训练A和B中的参数。如图所示,对于\(h=W_{0}x\),前向传播过程就变为: \[ h=W_0x+\Delta Wx=W_0x+BAx \]
三、QLORA
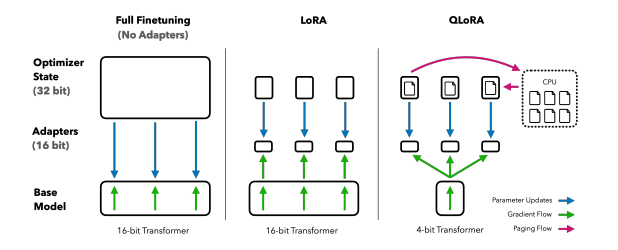
QLORA训练过程和LORA基本一致,区别在于QLORA模型是按照NF4保存的,训练时需要将参数反量化到bf16后进行训练。 \[ Y^{BF16}=X^{BF16}doubleDequant(c_{2}^{FP32},c_{2}^{k-bit},W^{NF8} )+X^{BF16}B^{BF16}A^{BF16} \]
分块量化(Block-wis Quantization)
量化是将输入从存储更多信息的表征映射为存储较少信息的表征的过程。
全局量化的方式存在一个问题:当输入中存在极大值或者离群值时,一些较小的参数无法被精确的表示,从而导致量化后的神经网络效果急剧下降。
分块量化是将输入划分为多个块,每个块分别量化,如图所示:
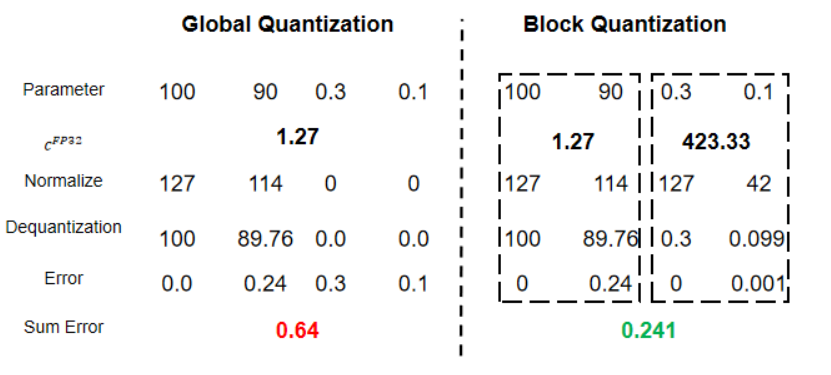
明显看到分块量化能够减少过程中的误差。
分位量化(Quantile Quantization)
在将一个参数量化到4bit的情境中,最多可以使用\(2^4\)一共16个数字。按照传统的简易方法,一般是取最接近的数字或者直接round函数。分位量化则是将数字按顺序排列,再分为十六等分,最小的一块映射成量化后的第一个数,第二块映射成量化后的第二数,以此类推。这样就充分利用了已有的数位,原始数据在量化后的数字上分布也是均匀的。
4-bit NormalFloat(NF4)
这个概念是在分位量化的基础上进行改进,并结合分块量化,降低计算复杂度和误差。上述的分位量化会增加计算消耗,预训练模型的参数基本上都服从均值为0的正态分布,可以将其缩放到[-1,1]的范围内。同时可以在[-1,1]的范围内,将正态分布函数划分为\(2^k +1\)份,直接将参数映射到对应的分位上,不用每次都进行排序。
双重量化(double Quantization)
分块量化中每个块都会额外产生一个量化常数c,以块大小为64为例,每个块会产生32bit的量化常数,双重量化则是在第一次量化后,不会直接存储量化常数\(C_1\),而是按照块大小256对量化常数再量化为8bit去存储,这个阶段会产生一个量化常数\(C_2\)。最终存储的参数为\(8/64 +32/(64-256)=0.127bits\).
四、AdaLORA
技术背景
LORA技术预先规定每个增量矩阵\(\Delta\)的秩必须相同,这就忽略了不同层、类型参数对下游任务的影响。
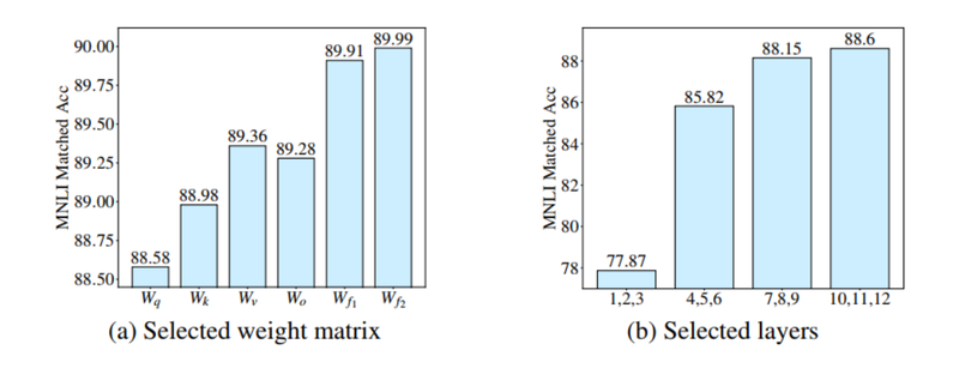
如图所示,将微调参数放在FFN的效果优于放在Attention矩阵中的效果;同时微调高层参数的效果优于微调底层参数。那么如何根据下游任务自动地找出重要的参数模块并给其分配更多地可微调参数呢?
解决方案
AdaLORA主要包含两个模块:
SVD形式参数更新(SVD-based adaptation):直接将增量矩阵\(\Delta\)参数化为SVD地形式,避免在训练过程中进行SVD计算带来的计算资源消耗;
根据重要程度地参数分配(Importance-aware rank allocation):去除一些冗余的奇异值。
\[ W=W^{(0)}+\Delta=W^{(0)}+P\Lambda Q \]
\[ R(P,Q)=||P^TP-I||_F^2+||Q^TQ-I||_F^2 \]
如式(5),AdaLORA增量矩阵\(\Delta\)替换为\(P\Lambda Q\),这样既省去复杂的SVD计算又能去除奇异值。同时,为保证P和Q的正交性,在训练过程中增加了一个正则化,保证\(P^{T}P=Q^{T}Q=I\).
该方法相较于LORA有两个优点:
- AdaLORA只去除奇异值矩阵,并不会去除奇异向量,更容易恢复误删的奇异值。
- AdaLORA的P和Q为正交举证,LORA的A和B矩阵非正交。训练过程中裁剪操作不会影响其他奇异值对应的奇异向量,训练会更稳定,泛化性能更好。
参考文章:
LORA微调系列(一):LORA和它的基本原理 - 知乎 (zhihu.com)