遗传算法
遗传算法(genetic algorithm)
1、概述
算法的主要思想就是模拟生物的遗传与变异,快速的求出最大值或最小值的随机全局搜索优化方法。
2、前置知识
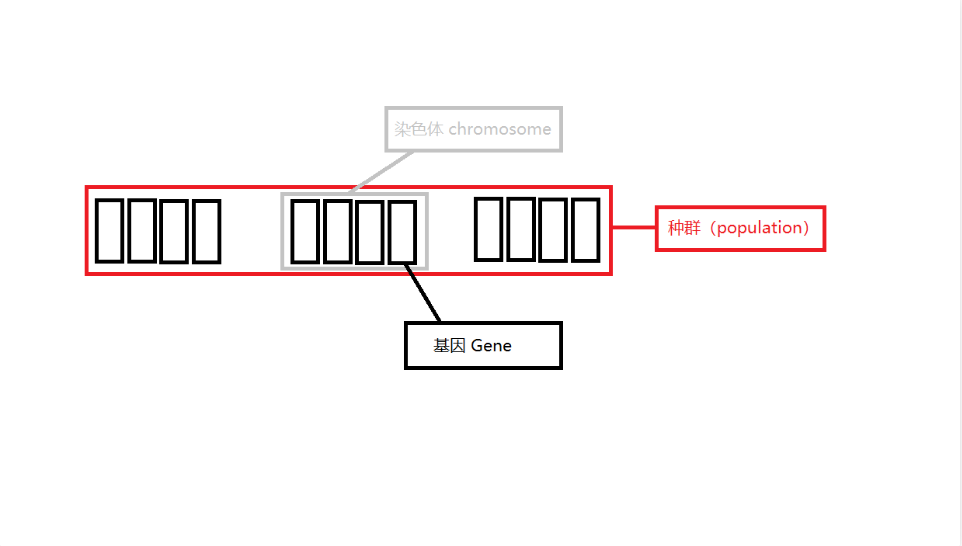
染色体(Chromosome):又称为基因型个体。
个体(individual):每个生物
种群(population):一个系统中所有个体的总称。
种群个体数(POPULATION):一个系统中个体的数量。
基因(gene):控制生物的性状。
适应度(fitness):对某个生物是否适应环境的定量评分。
迭代次数(TIMES):该生物种群繁衍的次数。
3、算法基础
基本遗传算法是将群体中所有个体作为对象,只使用基本遗传算子:选择算子、交叉算子以及变异算子。可以用一个式子表示: \[ SGA=(C,E,P_0,M,\phi,\Gamma,\psi,T) \]
| 符号 | 含义 |
|---|---|
| \(E\) | 个体适应度评价函数 |
| \(p_0\) | 初始种群 |
| \(C\) | 个体编码方案 |
| \(M\)(预先设定) | 种群大小 |
| \(\phi\) | 选择算子 |
| \(\Gamma\)(预先设定交叉概率) | 交叉算子 |
| \(\psi\)(预先设定变异概率) | 变异算子 |
| \(T\)(预先设定) | 遗传算法终止条件 |
4、算法步骤
4.1 染色编码
编码
将问题解空间的解表示为遗传算法中的染色体结构数据。常见的方法有:二进制编码、格雷码编码、 浮点数编码、各参数级联编码、多参数交叉编码等。
解码
将遗传算法染色体转换为问题的解.
4.2 初始群体的生成
设定最大进化迭代数T,群体大小M,交叉概率\(P_c\),变异概率\(P_m\),随机生成M个个体作为初始化群体\(P_0\).
4.3 适应度评估检测
适应度函数表明个体或解的优劣性。
适应度尺度变换:指算法迭代的不同阶段,通过适当调节个体适应度大小,避免群体间竞争减弱,导致种群收敛于局部最优解。
尺度变化的方法:
线性尺度变换:\(F^{\prime}=aF+b\)
乘幂尺度变换:\(F^{\prime}=F^{k}\)
指数尺度变换:\(F^{\prime}=e^{-\beta F}\)
4.4 遗传算子
选择:从旧群体中按照一定概率选择优良个体组成新种群,繁殖得到下一代个体。个体的选择与适应度(\(f\))正相关: \[ P_i=\frac{f_i}{\sum_{k=1}^Mf_k} \]
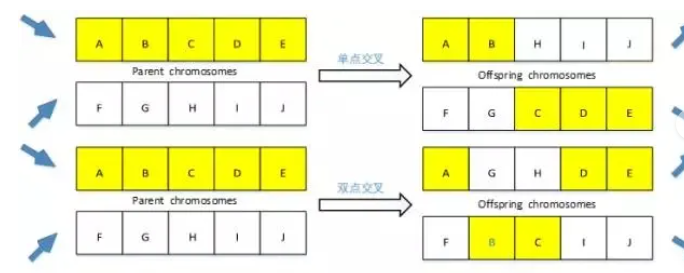
交叉:从种群中随机选择两个个体,随机选择点位,两个染色体交换组合,将父串的优秀特征遗传给子串,从而产生新的优秀个体。
方法包括单点交叉、双(多)点交叉、均匀交叉、算数交叉。
- 变异:以二进制编码为例:一段基因序列中的某位由0变为1,则称该点发生了变异。该方法可以防止算法在优化过程中陷入局部最优解。

4.5 终止判断条件
当\(t>T\)时,算法停止,选用前\(T\)步中具有最大适应度的个体作为输出。
