Attention机制
Attention机制
一、概述
Attention机制:对于某个时刻的输出y,他在输入x上各个部分上的注意力(也可以称之为权重),即输入x的各部分对某时刻输出y贡献的权重。目的就是让模型更关注需要关注的信息。
二、经典Attention机制
以经典\(Seq2Seq\)翻译模型为例,\(Seq2Seq\)结构包含两个部分:Encoder和Decoder,分别用于对语句进行编码和解码。
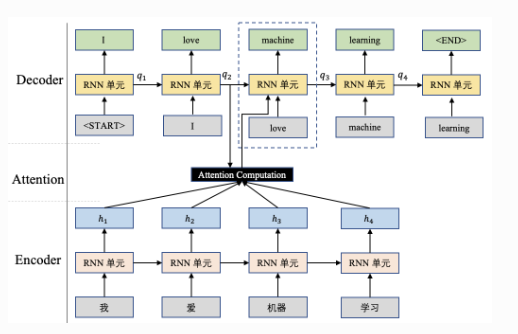
如图所示是生成单词\(machine\)的计算方式: \[ [a_1,a_2,a_3,a_4]=softmax([s(q_2,h_1),s(q_2,h_2),s(q_2,h_3),s(q_2,h_4)])context\quad=\sum_{i=1}^4a_i\cdot h_i \] 将前一时刻的输出状态\(q_2\)和Encoder输出进行Attention计算,得到一个context。其中\(s(q_i,h_j)\)表示注意力打分函数,表示当前时刻对Encoder结果的关注程度。
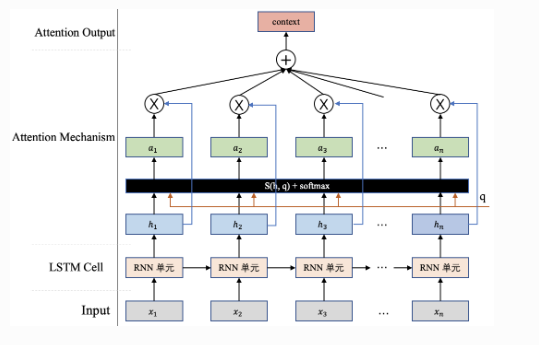
上图为抽象出的Attention原理图。假设有一组输入\(H=[h_1,h_2,h_3,\ldots,h_n]\)输入上述流程,需要一个Query向量\(q\)(这个向量往往和你做的任务有关,比如上述例子中用到的\(q_2\)),通过一个打分函数计算Query向量和每个输入\(h_i\)之间的相关性,得出一个分数并进行softmax归一化,最终得到Query向量\(q\)在各输入\(h_i\)上的注意力分布\(a=[a_1,a_2,a_3,\ldots,a_n]\)。 \[ a_i=softmax(s(h_i,q))=\frac{exp(s(h_i,q))}{\sum_{j=1}^nexp(s(h_j,q))} \] 最后根据注意力分布有选择的提取输入中的信息。这种方式是一种“soft”的信息提取方式,即根据注意力分布对输入信息进行加权求和,最终得到的context体现了模型当前应该关注的内容:\(context=\sum_{i=1}^na_i\cdot h_i\)
对于打分函数有以下几种形式:
加性模型:\(s(h,q)=v^Ttanh(Wh+Uq)\)
点积模型:\(s(h,q)=h^Tq\)相较于加性模型有更好的计算效率
缩放点积模型:\(s(h,q)=\frac{h^{T}q}{\sqrt{D}}\)当输入维度较高时,相较于点积模型拥有更好的平滑性
双线性模型:\(s(h_i,q)=h^TWq=h^T(U^TV)q=(Uh)^T(Vq)\)
上述公式中的参数(\(W、U、v\))均为可学习的参数矩阵或向量,\(D\)为输入向量的维度。
三、一些变体
Hard Attention
该方法时根据注意力分布选择输入向量中的一个作为输入,有两种选择方式:
- 选择注意力分布中,分数最大的那一项对应的输入向量作为Attention机制的输出。
- 根据注意力分布进行随机采样,采样结果作为Attention机制的输出。
这两种方式的输出会导致损失函数与注意力分布之间的函数关系不可导,无法使用反向传播算法训练模型,该机制通常需要使用强化学习进行训练。
key-value pair
当输入信息变为\((K,V)=[(k_1,v_1),(k_2,v_2),\ldots,(k_n,v_n)]\),这种模式下一般会使用Query向量和相应的键\(k_i\)进行计算权值\(a_i\)。
multi-head attention
该方法是利用多个Query向量\(Q=[q_1,q_2,\ldots,q_m]\),并行地从输入信息\((K,V)=[(k_1,v_1),(k_2,v_2),\ldots,(k_n,v_n)]\)中选取多组信息。在查询过程中,每个Query\(q_i\) 将会关注输入信息的不同部分。 \[ \begin{aligned} a_{ij}=softmax(s(k_j,q_i))& =\frac{exp(s(k_j,q_i))}{\sum_{t=1}^nexp(s(k_t,q_i))} \\ context_i& =\sum_{j=1}^na_{ij}\cdot v_j \end{aligned} \] \(a_{ij}\)表示第\(i\)个Query向量\(q_i\)与第\(j\)个输入信息\(k_j\)的注意力权重。
最终将所有Query向量进行拼接作为最终的结果: \[ context=context_1\oplus context_2\oplus context_3\oplus\ldots\oplus context_m \]
四、Self-Attention
在上述内容中提及的Query向量往往和任务相关,然而在self-attention中,Query向量可以使用输入信息进行生成,相当于模型读取输入信息后,根据信息本身决定当前最重要的信息。
自注意力机制往往采用\(Query-Key-Value\)的模型,以BERT中为例:
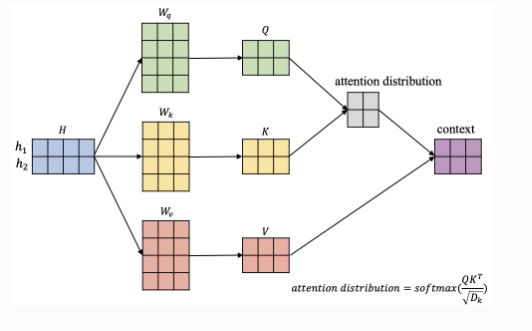
如图所示:输入信息\(H=[h_1,h_2]\),蓝色矩阵每行对应一个输入,\(W_q,W_k,W_v\)负责将输入信息分别转换到对应的Query空间、Key空间和Value空间: \[ \begin{gathered}\begin{bmatrix}q_1=h_1W_q\\q_2=h_2W_q\end{bmatrix}\Rightarrow Q=HW_q\\\\\begin{bmatrix}k_1=h_1W_k\\k_2=h_2W_k\end{bmatrix}\Rightarrow K=HW_k\\\\\begin{bmatrix}v_1=h_1W_v\\v_2=h_2W_v\end{bmatrix}\Rightarrow V=HW_v\end{gathered} \] 以\(h_1\)为例,计算该位置上的attention输出向量\(context_1\),来展示具体过程(下图流程中分数计算采用的是点积操作。\(D_k\)是\(Q、K\)矩阵的列数,即向量维度):

根据上图self-attention的输出向量计算过程可以总结成一个经典公式: \[ context=softmax(\frac{QK^T}{\sqrt{D_k}})V \]
相关经典问题
为什么要对\(QK^T\)进行scaling
如果不进行scaling,当\(D_k\)增大时,\(QK^T\)的方差会增大\(\sqrt{D_k}\)倍。而\(QK^T\)作为\(softmax\)的输入如果增大容易导致梯度消失。
self-attention表达是固定嘛
不一定,只要可以建模相关性就可以。最好是能够高速计算(矩阵乘法),并且表达能力强,模型容量够。
是否有其他方法不用除\(\sqrt{D_k}\)
有,只要能缓解梯度消失的问题就可以,例如\(T5\)模型的\(Xavier\)初始化。\(Xavier\)初始化试图让神经网络每一层的输出的方差接近于其输入的方差。具体而言,该方法将权重\(w\)的方差初始化为: \[ Var(w)=\frac{2}{n_{in}+n_{out}} \]
作用:
- 有效防止梯度消失或爆炸:Xavier 初始化试图使得每一层的输出的方差接近于其输入的方差,从而避免梯度消失或梯度爆炸的问题。
- 加速收敛:Xavier 初始化使得每一层的输出的方差接近于其输入的方差,从而使得每一层的梯度的方差接近于 1。这样,每一层的参数更新的幅度就不会相差太大,从而加速收敛。