盛水最多容器

盛最多水的容器

1、题目

image-20231224163543608

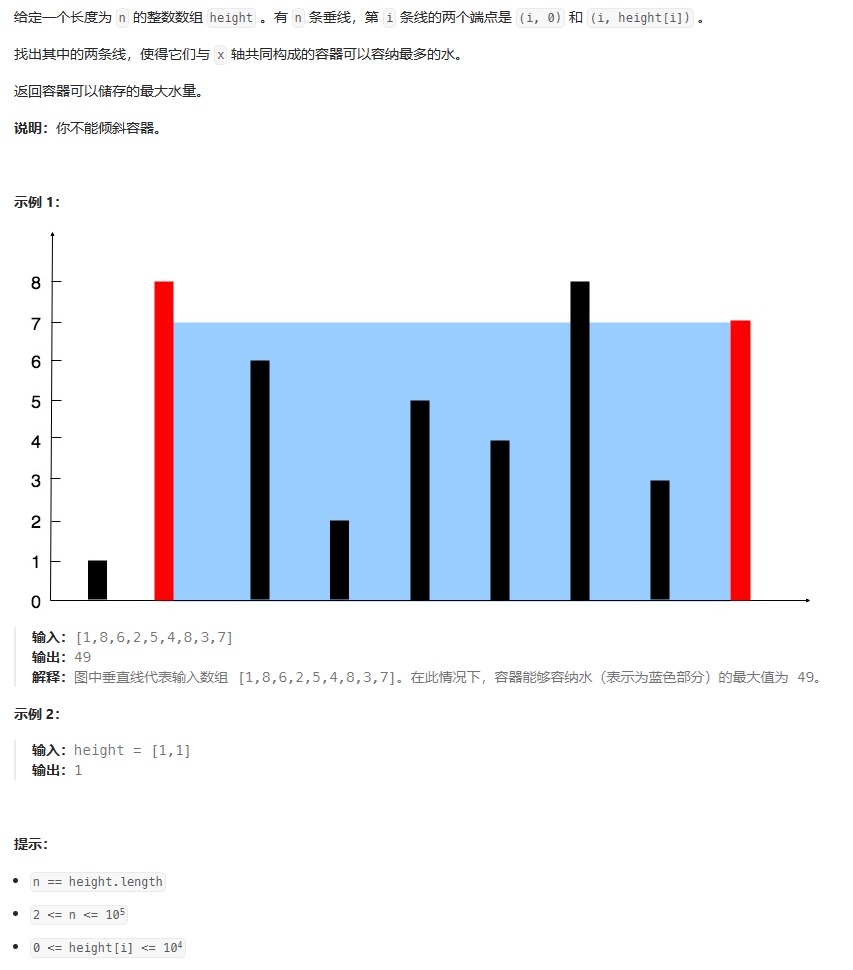
2、题解

双指针

思路：根据题目可以得到水槽面积公式为：\(S(i,j)=min(h[i],h[j])\times(j-i)\),其中\(h[i]\)表示水槽高度。在所有状态下，无论如何移动槽板，都会使水槽宽度\(-1\):

• 若向内移动短板 ，水槽的短板 \(min(h[i],h[j])\)可能变大，因此下个水槽的面积可能增大 。

• 若向内移动长板 ，水槽的短板 \(min(h[i],h[j])\) 不变或变小，因此下个水槽的面积一定变小 。

搞清迭代条件，我们就令双指针初始化为水槽左右两端，每轮迭代将短板向内移动一格，更新面积最大值，直到双指针相遇，结束迭代，得到最大面积。

# 官方题解
class Solution:
    def maxArea(self, height: List[int]) -> int:
        i, j, res = 0, len(height) - 1, 0
        while i < j:
            if height[i] < height[j]:
                res = max(res, height[i] * (j - i))
                i += 1
            else:
                res = max(res, height[j] * (j - i))
                j -= 1
        return res

# 自己写的
class Solution:
    def maxArea(self, height: List[int]) -> int:
        first = 0
        last = len(height)-1
        area = 0
        while(first != last):
            print(height[first])
            print(height[last])
            area = max(area, min(height[first],height[last])*(last-first))
            if height[first] >= height[last]:
                last = last -1
            else:
                first += 1

        return area

PS：与双for(一对双for走天下)相比

在暴力枚举的情况下水槽面积的状态总数为:\(C(n,2)\),向内移动短板至\(S(i+1,j)\),相当于跳过了\(S(i,j-1),S(i,j-2),……，S(i,i+1)\)状态集合。并且所有跳过的面积集合都一定小于当前面积，因为：

• 短板高度：相比 \(S(i, j)\) 相同或更短；

• 底边宽度：相比 \(S(i, j)\) 更短；

因此，每轮向内移动短板，所有消去的状态都 不会导致面积最大值丢失。

复杂度分析：

• 时间复杂度 O(N) ： 双指针遍历一次底边宽度 N 。
• 空间复杂度 O(1) ： 变量 i , j , res使用常数额外空间。