变分自编码器VAE(Variational Auto-Encoder)

变分自编码器的目标是构建一个根据隐藏变量生成目标数据的模型

假设有一组数据{\(x_1,x_2,…x_n\)},整体用\(X\)表示。理想情况下可以从数据中直接得到\(X\)的分布\(P(X)\)，根据\(P(X)\)进行采样可以得到所有可能的\(X\)。通常情况下很难实现上述所说的，而是将\(P(X)\)​改写为： \[ p(X)=\sum_Zp(X|Z)p(Z) \] \(p(X|Z)\)表示一个由Z来生成\(X\)的生成模型，假设已知\(Z\)服从正态分布，就可以根据\(Z\)来计算\(X\)。

img

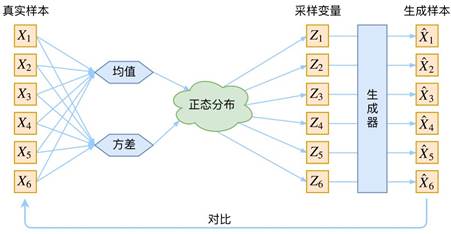
在\(VAE\)模型中，并没有直接假设\(p(Z)\)服从正态分布，而是假设\(p(Z|X)\)服从正态分布(对于一个真实样本\(X_k\),都存在一个专属于\(X_k\)的分布\(p(Z|X_k)\),方便后续进行从\(Z\)到\(X\)的精准映射)。

由上述可知有多少个\(X\)就有相应数量的正态分布，可以借助神经网络来拟合分布的均值和方差。构建两个网络：\(μ_k=f_1(X_k), log\sigma^2=f_2(X_k)\)。拟合\(log\sigma^2\)是因为\(\sigma^2\)非负，需要激活函数处理。

根据上述过程可以得到每个数据的专属生成器，\(VAE\)示意图如下图所示：

变分自编码器（Variational Auto-Encoder，VAE） | 望江人工智库

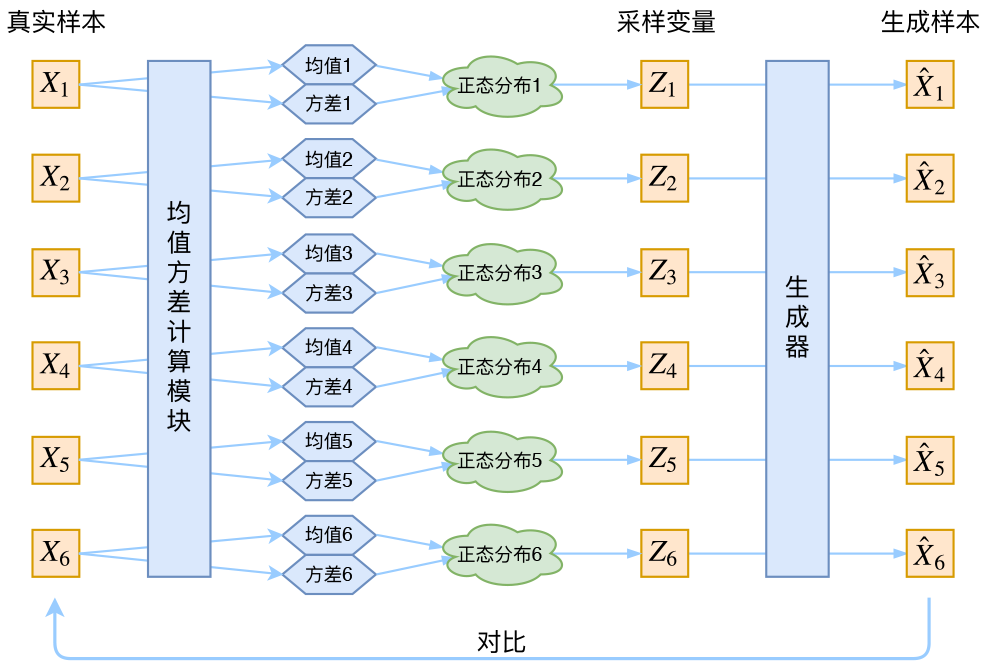
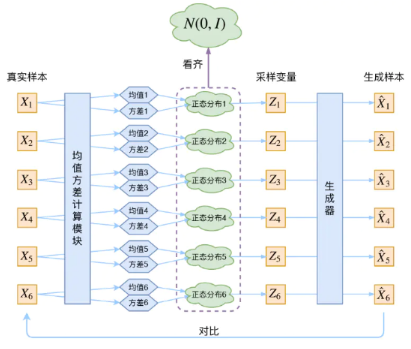
重构\(X\)的目的是最小化\(D(\hat{X}k,Xk)^2\),这个过程中会受到噪声影响，因为\(Z_K\)是通过采样的，而不是直接由encoder编码出来的。为了保证采样的随机性 ，\(VAE\)让所有\(p(Z|X)\)​都对齐标准正态分布，这样防止噪声为0，同时保证模型具备生成能力： \[ p(Z)=\sum_Xp(Z|X)p(X)=\sum_X\mathcal{N}(0,I)p(X)=\mathcal{N}(0,I)\sum_Xp(X)=\mathcal{N}(0,I) \] 这样就从而实现了先验分布\(P(Z)\)是标准正态分布，从而进行采样。

image-20240131153443961