接雨水

1、题目

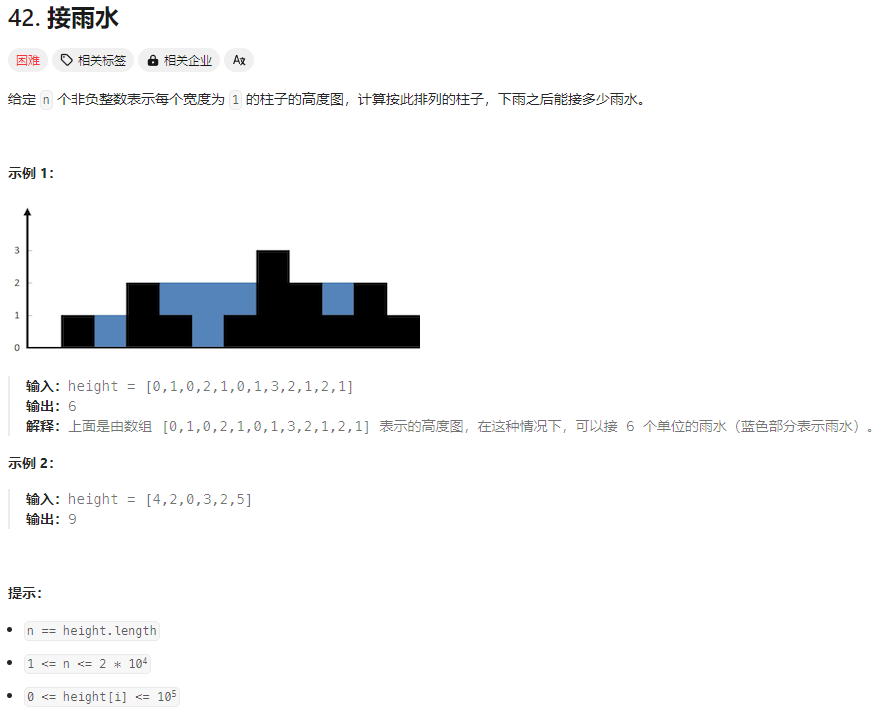image-20240222201820556

2、题解

1、动态规划

对于下标\(i\)，下雨后能接到的雨水等于下标i两边的最大高度的最小值减去\(height[i]\)。通常的方法是分别向左向右扫描并记录每个下标左右边的最大高度，然后计算每个下标位置能接的雨水量。这种做法的时间复杂度为\(O(n^2)\)。为了避免对每个下标位置进行双边扫描，换作对每个位置两边的最大高度进行扫描。

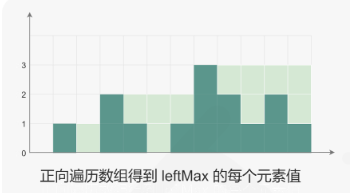image-20240222202616303

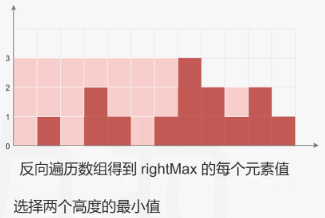image-20240222202633255

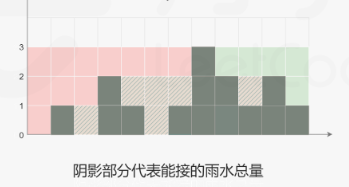image-20240222202649986

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0
        h_len = len(height)

        leftMax = [height[0]] + [0]*(h_len-1)

        for i in range(1,h_len):
            leftMax[i]= max(leftMax[i-1], height[i])
        
        rightMax = [0]*(h_len-1) + [height[h_len-1]]

        for i in range(h_len-2, -1, -1):
            rightMax[i] = max(rightMax[i+1], height[i])

        sum_rain = 0
        for i in range(h_len):
            every_rain = min(leftMax[i],rightMax[i])-height[i]
            sum_rain += every_rain
        
        return sum_rain

2、双指针

下标\(i\)处能接到的雨水量是由\(leftMax[i]\)和\(rightMax[i]\)中的最小值决定，由于两个数组分别是从左往右和从右往左计算，因此可以用双指针和两个变量代替两个数组。初始时，将指针初始化为\(left=0，right=n-1，leftMax=0,rightMax=0\)。当两个指针没有相遇时：

• \(用height[left]、height[right]的值更新leftMax、rightMax的值\)
• \(当height[left]<height[right]，则必有leftMax<rightMax，下标处能接到的与水量等于leftMax-height[left]，将该雨水量加入能接到的雨水总量，然后left+1;\)
• \(当height[left]≥height[right]，则必有leftMax≥rightMax，下标处能接到的与水量等于rightMax-height[right]，将该雨水量加入能接到的雨水总量，然后right-1;\)

当两个指针相遇时，得到的即是能接到的雨水总量。

class Solution:
    def trap(self, height: List[int]) -> int:
        ans = 0
        left, right = 0, len(height) - 1
        leftMax = rightMax = 0

        while left < right:
            leftMax = max(leftMax, height[left])
            rightMax = max(rightMax, height[right])
            if height[left] < height[right]:
                sum_rain += leftMax - height[left]
                left += 1
            else:
                sum_rain += rightMax - height[right]
                right -= 1
        
        return sum_rain