搜索二维矩阵

1、题目

图1

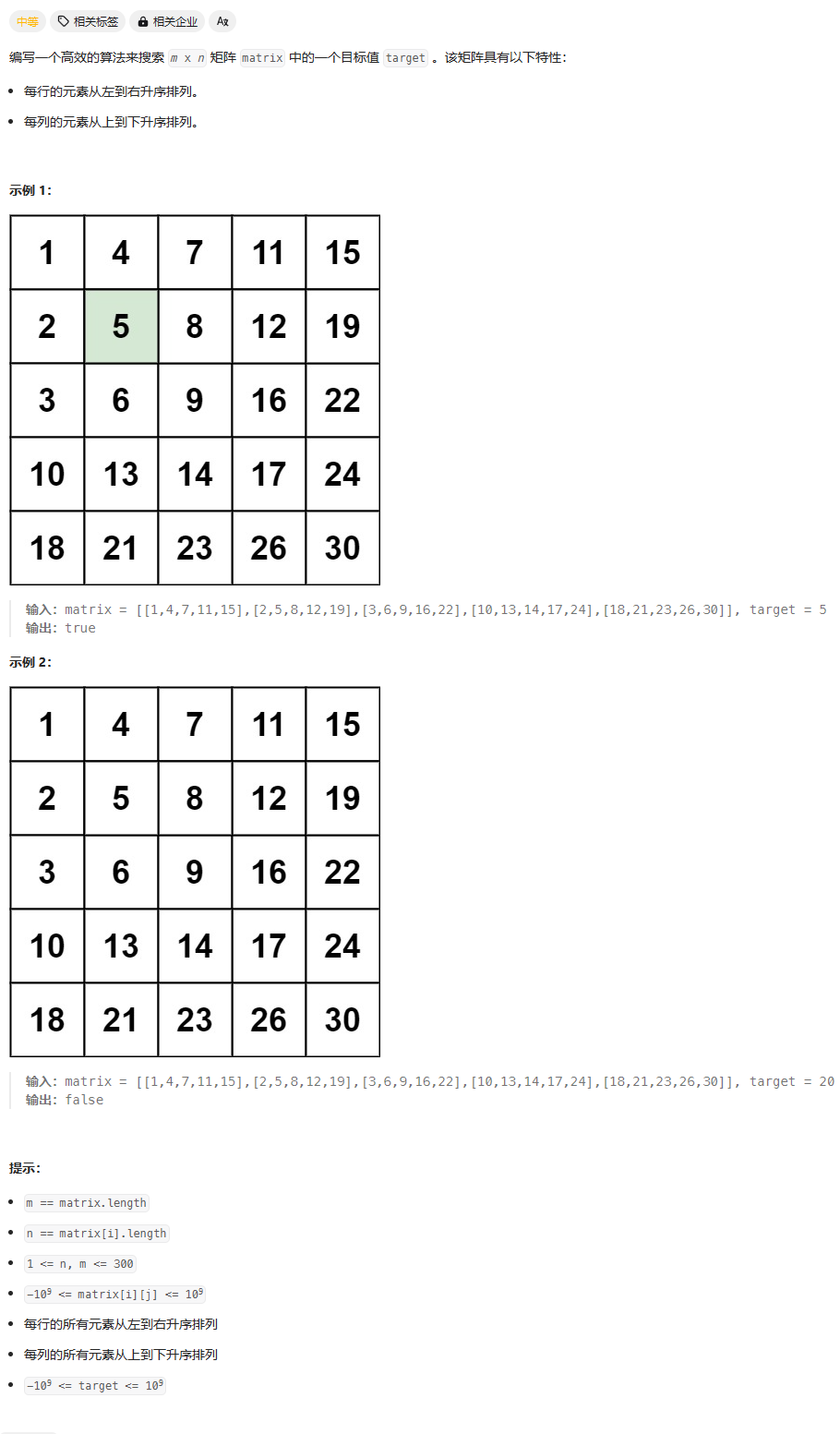
2、题解

贪心

利用矩阵从左到右、从上到下依次递增的特性，可以发现矩阵的结构类似于二叉搜索树。根节点对应矩阵左下角和右上角的元素，若以矩阵左下角元素为标志数flag：

• 若\(flag>target\),则\(targe\)t一定在\(flag\)所在行的上方，\(flag\)所在行可被消去
• 若\(flag<target\),则\(target\)一定在\(flag\)所在列的右方，\(flag\)​所在列可被消去

从矩阵左下角元素开始遍历，与目标值进行比对：

• 当\(matrix[i][j]>target\)时，执行\(i--\),消去第i行元素
• 当\(matrix[i][j]<target\)时，执行\(j++\),消去第j列元素
• 当\(matrix[i][j]=target\)时，返回True

若行或列索引越界，则代表矩阵中无目标值，返回False

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        i, j = len(matrix) - 1, 0
        while i >= 0 and j < len(matrix[0]):
            if matrix[i][j] > target: i -= 1
            elif matrix[i][j] < target: j += 1
            else: return True
        return False