二叉树最大深度

二叉树的最大深度

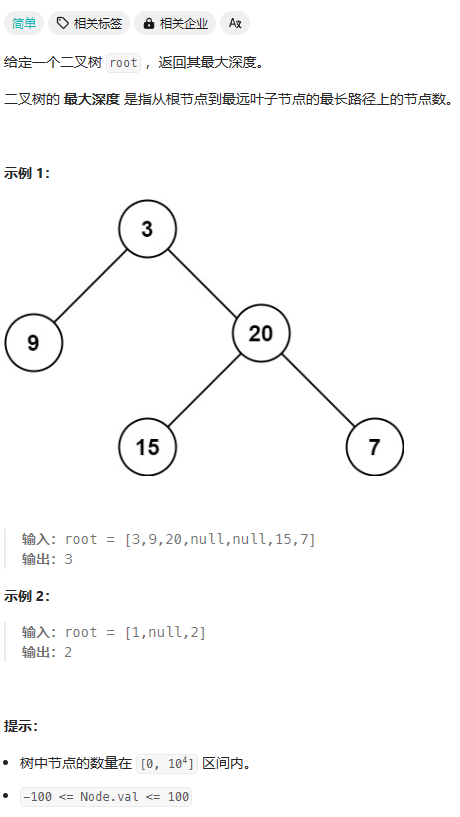
1、题目

图1

2、题解

树的遍历方式总体分为两类：深度优先搜索(DFS)、广度优先搜索(BFS)

• 常见DFS：先序遍历、中序遍历、后序遍历
• 常见BFS：层序遍历

后序遍历(递归)

树的深度等于左子树深度和右子树深度最大值加1

算法流程：

终止：当root为空，表明越过叶节点，返回深度0

递归：计算root的左子树深度，即调用\(函数(root.left)\)；计算root的右子树深度，即调用\(函数(root.right)\)

返回：返回节点树的深度，即\(max(函数(root.left),函数(root.right))+1\)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root: return 0
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
        

层序遍历(队列)

每遍历一层，深度加1，直至遍历完成

算法流程：

• 当root为空，返回深度0
• 初始化队列que(加入根节点)，深度res=0
• 遍历：当que为空时结束。
  • 初始化一个空列表tmp，用于临时存储下一层的节点。
  • 遍历que中的各节点，将其左右子节点加入tmp
  • 令que=tmp
  • 深度加1
• 返回res

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root: return 0
        res = 0
        que = [root]
        while que:
            tmp = []
            for node in que:
                if node.left: tmp.append(node.left)
                if node.right: tmp.append(node.right)
            
            que = tmp
            res += 1
        
        return res