RoPE——旋转式位置编码

旋转式位置编码(Rotary Position Embedding，RoPE)

实现思路

该技术的出发点是通过绝对位置编码方式实现相对位置编码，该方法在理论和实践上都有一定的道理。

假设通过下述运算给\(q,k\)​添加绝对位置信息： \[ \tilde{\boldsymbol{q}}_m=\boldsymbol{f}(\boldsymbol{q},m),\quad\tilde{\boldsymbol{k}}_n=\boldsymbol{f}(\boldsymbol{k},n) \] 通过分别为\(q,k\)设计函数\(\boldsymbol{f}(\cdot,m),\boldsymbol{f}(\cdot,n)\),使得经过该函数后，\(\tilde{\boldsymbol{q}}_m,\tilde{\boldsymbol{k}}_n\)就带有\(m,n\)​的绝对位置信息。Attention的核心运算是内积，因此希望内积后的结果带有相对位置信息，所以假设存在恒等关系： \[ \langle\boldsymbol{f}(\boldsymbol{q},m),\boldsymbol{f}(\boldsymbol{k},n)\rangle=g(\boldsymbol{q},\boldsymbol{k},m-n) \] 根据上述等式可以求出一个解。

求解过程

可以合理设初始条件\(\boldsymbol{f}(\boldsymbol{q},0)=\boldsymbol{q},\boldsymbol{f}(\boldsymbol{k},0)=\boldsymbol{k}\)​，以二维情况为例：

在复数中有\(\langle\boldsymbol{q},\boldsymbol{k}\rangle=\mathrm{Re}[\boldsymbol{q}\boldsymbol{k}^{*}]\)，所以可以得到：\(\operatorname{Re}[\boldsymbol{f}(\boldsymbol{q},m)\boldsymbol{f}^*(\boldsymbol{k},n)]=g(\boldsymbol{q},\boldsymbol{k},m-n)\)。假设存在复数\(g(\boldsymbol{q},\boldsymbol{k},m-n)\)，使得\(\boldsymbol{f}(\boldsymbol{q},m)\boldsymbol{f}^*(\boldsymbol{k},n)=\boldsymbol{g}(\boldsymbol{q},\boldsymbol{k},m-n)\)​,根据复数的指数形式可以令： \[ \begin{aligned} f(\boldsymbol{q},m)& =R_{f}(\boldsymbol{q},m)e^{\mathrm{i}\Theta_{f}(\boldsymbol{q},m)} \\ \boldsymbol{f}(\boldsymbol{k},n)& =R_f(\boldsymbol{k},n)e^{\mathrm{i}\Theta_f(\boldsymbol{k},n)} \\ \boldsymbol{g}(\boldsymbol{q},\boldsymbol{k},m-n)& =R_g(\boldsymbol{q},\boldsymbol{k},m-n)e^{\mathrm{i}\Theta_g(\boldsymbol{q},\boldsymbol{k},m-n)} \end{aligned} \] 将(3)代入方程可以得到： \[ \begin{aligned}R_f(\boldsymbol{q},m)R_f(\boldsymbol{k},n)&=R_g(\boldsymbol{q},\boldsymbol{k},m-n)\\\Theta_f(\boldsymbol{q},m)-\Theta_f(\boldsymbol{k},n)&=\Theta_g(\boldsymbol{q},\boldsymbol{k},m-n)\end{aligned} \] 对于第一个式子，当\(m=n\)时，可以得到：\(R_f(\boldsymbol{q},m)R_f(\boldsymbol{k},m)=R_g(\boldsymbol{q},\boldsymbol{k},0)=R_f(\boldsymbol{q},0)R_f(\boldsymbol{k},0)=\|\boldsymbol{q}\|\|\boldsymbol{k}\|\)

根据上式可以设\(R_f(\boldsymbol{q},m)=\|\boldsymbol{q}\|,R_f(\boldsymbol{k},m)=\|\boldsymbol{k}\|\)，从式子中可以看到二者都不依赖于m。

同理对第二个式子：\(\Theta_f(\boldsymbol{q},m)-\Theta_f(\boldsymbol{k},m)=\Theta_g(\boldsymbol{q},\boldsymbol{k},0)=\Theta_f(\boldsymbol{q},0)-\Theta_f(\boldsymbol{k},0)=\Theta(\boldsymbol{q})-\Theta(\boldsymbol{k})\)

根据上式可以看出\(\Theta_{f}(\boldsymbol q,m)-\Theta(\boldsymbol q)\)应该是一个只与m相关、跟q无关的函数，记作\(\varphi(m)\)。所以\(\Theta_{f}(\boldsymbol q,m)=\Theta(\boldsymbol q)+\varphi(m)\)​。令n=m-1，可以得到： \[ \varphi(m)-\varphi(m-1)=\Theta_g(\boldsymbol{q},\boldsymbol{k},1)+\Theta(\boldsymbol{k})-\Theta(\boldsymbol{q}) \] 即{\(\varphi(m)\)}为等差数列，令(5)右边式子为\(\theta\)，可以得到$=m $

编码形式

根据上述推导可以得到二维情况下RoPE表达式： \[ f(\boldsymbol{q},m)=R_f(\boldsymbol{q},m)e^{\mathrm{i}\Theta_f(\boldsymbol{q},m)}=\|q\|e^{\mathrm{i}(\Theta(\boldsymbol{q})+m\theta)}=\boldsymbol{q}e^{\mathrm{i}m\theta} \] 根据复数乘法的几何意义，该变化实际上对应向量的旋转，上式可以写成矩阵形式： \[ \left.\boldsymbol{f}(\boldsymbol{q},m)=\left(\begin{array}{cc}\cos m\theta&-\sin m\theta\\\sin m\theta&\cos m\theta\end{array}\right.\right)\left(\begin{array}{c}q_0\\q_1\end{array}\right) \] 由于内积满足线性叠加性，因此任意偶数维的RoPE，都可以表示为二维情形的拼接：

图1

给位置m的向量q乘上矩阵\(W_m\)、位置n的向量k乘上矩阵\(W_n\)，用变换后的\(Q、K\)​进行attention计算，可以得到： \[ (\boldsymbol{W}_m\boldsymbol{q})^\top(\boldsymbol{W}_n\boldsymbol{k})=\boldsymbol{q}^\top\boldsymbol{W}_m^\top\boldsymbol{W}_n\boldsymbol{k}=\boldsymbol{q}^\top\boldsymbol{W}_{n-m}\boldsymbol{k} \] \(W_m\)是一个正交矩阵，它不会改变向量模长，因此通常讲不会改变模型的稳定性。由于\(W_m\)​的稀疏性，直接矩阵乘法实现会浪费算力，可以通过下述式子实现：

图2

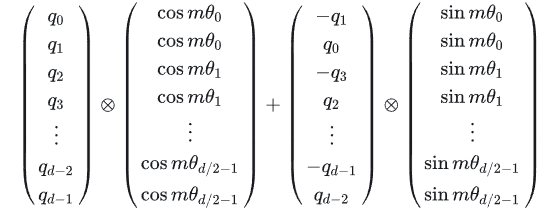
$$表示逐位对应相乘。

远程衰减

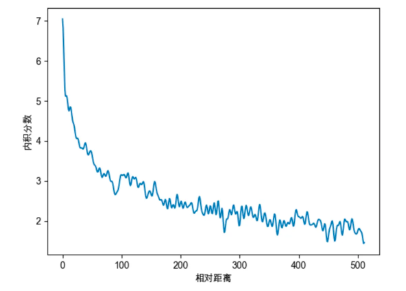
与Sinusoidal位置编码相比，RoPE编码在形式上相似，不过前者是加性的，而后者可以看作是乘性。在\(\theta_i\)的选择上沿用了Sinusoidal位置编码的方案，即\(\theta_{i}=10000^{-2i/d}\)​，这会导致一定的远程衰减性。例如将q固定在位置0处，k的位置从0开始增大，依次计算内积：

图3

对于\(\theta_{i}\)的取值可以进一步探究，令\(\theta_{i}=base^{-2i/d}\)，其中改变base的取值：

图4

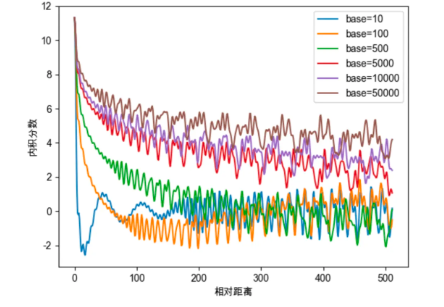
从图4中可以看出base的不同取值会影响注意力远程衰减的程度。当base大于500时，随着base的提升，远程衰减的程度会逐渐削弱。但太小的base也会破坏注意力远程衰减的性质，例如base=10或100时，注意力分数不再随着相对位置的增大呈现出震荡下降的趋势。极端的情况下，当base=1时，将完全失去远程衰减特性：

图5

对于base的性质研究与大模型的长度外推有很大关系，如NTK-Aware Scaled RoPE、NTK-by-parts、Dynamic NTK等长度外推方法，本质上都是通过改变base，从而影响每个位置对应的旋转角度，进而影响模型的位置编码信息，最终达到长度外推的目的。目前大多长度外推工作都是通过放大base以提升模型的输入长度，但更大的base也将会使得注意力远程衰减的性质变弱，改变模型的注意力分布，导致模型的输出质量下降。

长度扩展

基于RoPE的大模型进行长度扩展的方法，大致可以分为两大类：局部注意力和调整旋转弧度。

调整旋转弧度

模型在训练时，只见过\([0,(L-1)\theta_i]\)范围内的旋转弧度，未见过大于\((L-1)\theta_i\)的旋转弧度，所以当推理长度大于 时，模型难以理解新的旋转弧度，无法正确注入位置信息，导致模型性能下降(这只是一个简单的说法)。

Position Interpolation

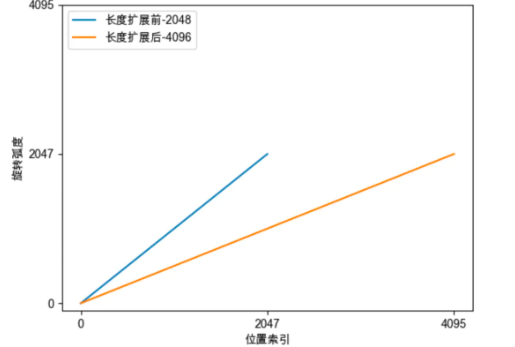
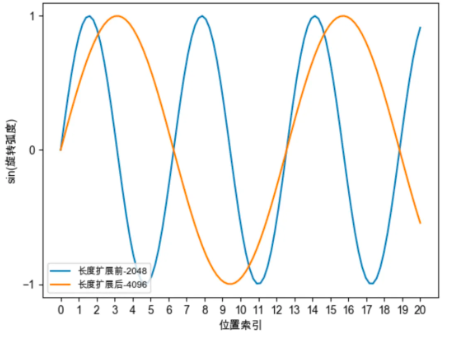
该做法简单直观：缩小每个位置的旋转弧度，让向量旋转得慢一些，每个位置的旋转弧度变为原来的\(\frac L{L^{\prime}}\)，长度扩大几倍，则旋转弧度缩小几倍。最终，经过调整后，位置\(m\)​的旋转弧度如下公式所示： \[ \frac{mL\theta_i}{L^{'}}=\frac{mL}{L^{'}}base^{-2i/d} \] Position Interpolation将每个位置的旋转弧度均变为原来的一半。这相当于在原来的弧度范围内，插入更多的位置，由于旋转弧度是线性变化的，所以也称为线性位置插值。进行位置插值后，向量旋转速度变慢，周期变大，频率变慢。

举个例子，将模型的长度从2048扩展至4096：

图6

图7

NTK-Aware Interpolation

作者认为高频信息对于神经网络非常重要，而Position Interpolation对于向量的所有分组不加区分地缩小旋转弧度，降低旋转速度（进一步体现为对其正弦函数进行拉伸），会导致模型的高频信息缺失，从而影响模型的性能。

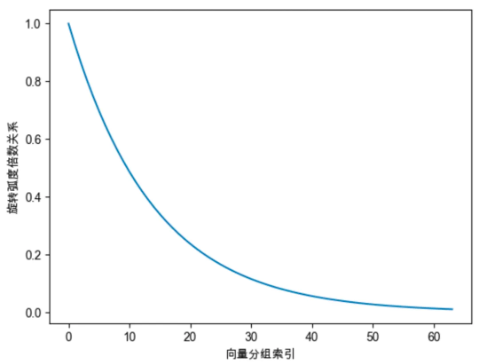
上面介绍过，位置越靠前的向量分组，旋转速度越快。频率越高。为了保留高频信息，在NTK-Aware插值中，经过调整后，位置\(m\)的旋转弧度如下公式所示，LLaMA中的 \(base=10000\)，\(\alpha\)表示缩放因子： \[ m\theta_i=m*(base*\alpha)^{-2i/d}=m*(10000*\alpha)^{-2i/d} \] 以Code LLaMA为例进行分析，Code LLaMA中 \(\alpha=100\)，表示将原始模型的\(base\)放大100倍，调整后的旋转弧度与原始旋转弧度的倍数关系如下： \[ \frac{m*(1000000)^{-2i/d}}{m*(10000)^{-2i/d}}=100^{-2i/d} \] 如下图所示，越靠后的分组，旋转弧度缩小的倍数越大。其中第0分组的旋转弧度保持不变，最后一个分组的旋转弧度变为原来的1/100。可以将NTK-Aware Interpolation的思想总结为：保留高频信息；高频分量旋转速度降幅低，低频分量旋转速度降幅高；在高频部分进行外推，低频部分进行内插：

图8

图9

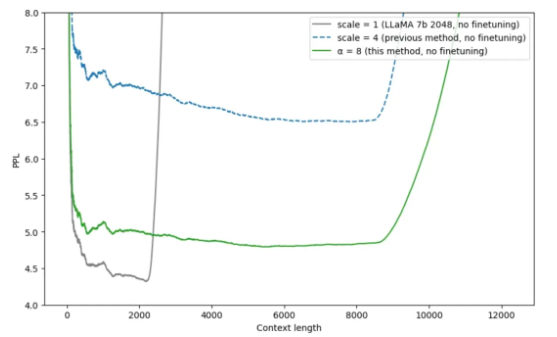
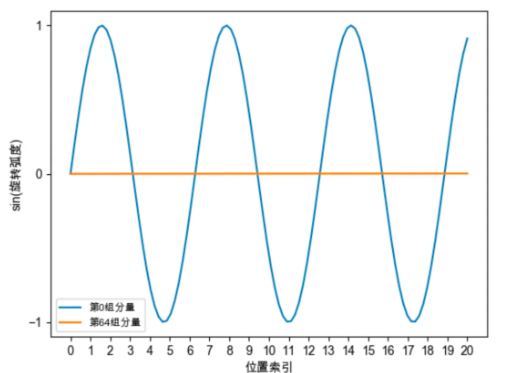
如图所示，在不进行finetune的时候，NTK-Aware插值的效果比线性插值更优。为什么NTK-Aware Interpolation能够奏效？上文提到过，位置越靠后的分组旋转速度越慢，频率越低，周期越长。如下图所示，对于第0组分量，仅在位置7时，就已经旋转一周。但对于第64组分量，当位置为2047时，其旋转弧度约为0.2047，甚至仍未完成1/4周旋转。

图10

综上所诉，将NTK-Aware Interpolation奏效的原因主要有两点：

1. 前置的分组在训练中见过很多完整的旋转周期，位置信息得到充分训练，所以具备较强的外推能力
2. 后置的分组在训练中无法见过完整的旋转周期，或者见到的旋转周期非常少，训练不够充分，外推能力弱，需要进行位置插值。

NTK-by-parts Interpolation

NTK-by-parts Interpolation则是基于NTK-Aware Interpolation进行优化，其核心思想是：不改变高频部分，仅缩小低频部分的旋转弧度。也就是不改变靠前分组的旋转弧度，仅减小靠后分组的旋转弧度，这就是by-patrs的含义。

第\(i\)​个分组的旋转周期如下： \[ \lambda_i=\frac{2\pi}{\theta_i}=2\pi*base^{2i/d} \] 第\(i\)个分组在训练长度内旋转的周期个数:\(r(i)=\frac{L}{\lambda_i}\)。以每组分量在训练长度内旋转的周期个数\(r(i)\)分类讨论插值方案。引入超参数\(\beta\)，表示旋转周期个数的约束条件。

Dynamic NTK Interpolation

Dynamic NTK Interpolation是一种动态插值的方法，思路很简单：推理长度小于等于训练长度时，不进行插值；推理长度大于训练长度时，每一步都通过NTK-Aware Interpolation动态放大base。当序列长度大于模型训练长度时，使用NTK-Aware Interpolation调整旋转弧度为\(m*(base*\alpha)^{-2i/d}\)，\(\alpha=\left(\frac{l}{L}\right)^{d/(d-2)}\)。超出模型序列长度后，每一次生成都会根据当前长度重新调整旋转弧度，然后再进行下一次生成。

YaRN

无论是Position Interpolation还是NTK类方法，本质都是通过减小旋转弧度，降低旋转速度，来达到长度扩展的目的。这将导致位置之间的旋转弧度差距变小，词向量之间的距离变得比原来更近，词向量之间的点乘变大，破坏模型原始的注意力分布。所以经过插值之后，模型在原来的训练长度内的困惑度均有所提升，性能受损。

根据向量内积公式(\(q.k=|q|*|k|*cos(\gamma)\))，向量旋转不改变模长，当旋转弧度变小，导致二者之间的夹角变小，从而内积变大，最终会影响模型的注意力分布。

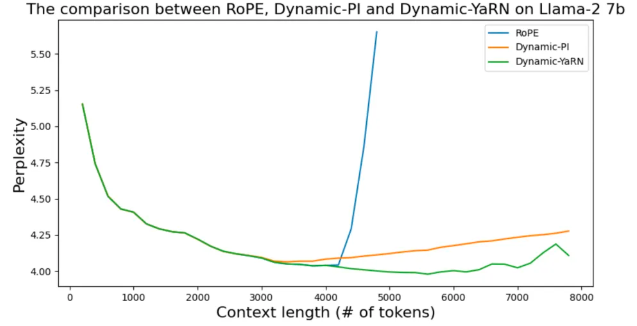
YaRN本质上是NTK-by-parts Interpolation与注意力分布修正策略的结合，仅缩小低频部分的旋转弧度，且通过温度系数修正注意力分布。只需将原来的注意力分数除以温度\(t\)​即可: \[ \dfrac{\mathbf{q}_m^T\mathbf{k}_n}{\sqrt{|d|}}\to\dfrac{\mathbf{q}_m^T\mathbf{k}_n}{t\sqrt{|d|}} , \sqrt{\dfrac1t}=0.1*\ln\!\left(\dfrac{L^{'}}{L}\right)+1 \] 下图是未经过微调的动态插值方法的比较，修正了注意力分布的Dynamic-YaRN，显著优于未修正注意力分布的Dynamic-PI方法。

图11