KVCache

1、为什么需要这个技术

对于LLM 类模型的一次推理(生成一个token)过程，可以将该过程分解为下列过程：

• 输入n个token\(\{T_{1},\cdots,T_{i},\cdots,T_{n}\}\),
• token预处理阶段，将token处理成token embedding\(\{x_{1}^{0},\cdots,x_{i}^{0},\cdots,x_{n}^{0}\}\)(上标表示模型第几层的输入),每个token embedding为一个向量，维度记为\(D\)。
• token embedding变换阶段，模型内部包含\(L\)层，每层的输入是token embedding，输出也是token embedding。最后一层输出的token embedding是\(\{x_{1}^{L},\cdots,x_{i}^{L},\cdots,x_{n}^{L}\}\)
• next token generation阶段，由最后一层的最后一个token embedding\(x^L_n\)，结合vocabulary embedding(lm_head)\(\{e_{1},\cdots,e_{i},\cdots,e_{V}\}\)，生成每个token的概率\(\{p_1,\cdots,p_i,\cdots,p_V\}\)，再根据概率分布采样得到一个具体的token\(T_{n+1}\)。

图1

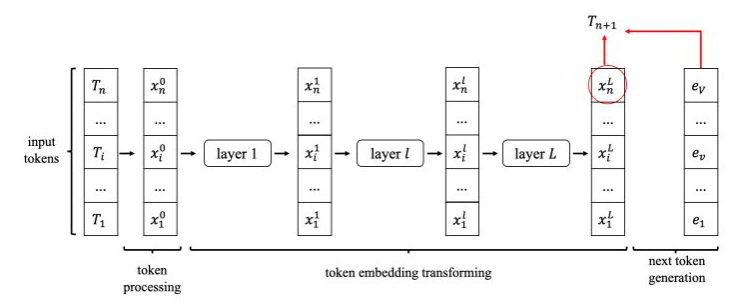
我们可以通过上面的流程接着生成下一个token，但是我们可以发现两次生成的计算之间存在可以复用的部分：在生成token embedding时，前T个token的embedding和上一轮的相同，可以通过复用上一轮的计算结果：

图2

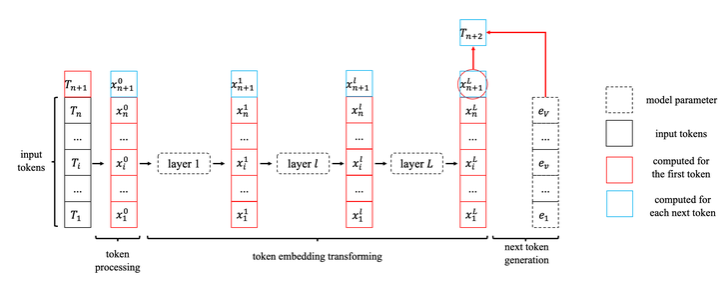
2、KVCache的原理及设计细节

当我们复用了中间结果时，每一层的计算输入为上次保存下来的\(\{x_{i}^{l}|1\leq i\leq n\}\)以及本次新来的\(x_{n+1}^l\)，需要计算得到的输出为\(x_{n+1}^{l+1}\)​。所以这是一个single-query attention计算，只关注最后一个token的输出，就可以得到： \[ \begin{aligned} s_{i}& =(W_Q x_{n+1}^l)^T(W_K x_i^l) ,1\leq i\leq n+1 \\ y_{h}& =\sum_{i=1}^{n+1}\frac{e^{s_{i}}}{\sum_{j=1}^{n+1}e^{s_{j}}}W_{V} x_{i}^{l} ,1\leq i\leq n+1 \\ x_{n+1}^{l+1}& =\mathrm{Concat}_{h=1}^H y_h \end{aligned} \] 根据这一公式，我们可以进一步看出，如果我们只保存\(\{x_{i}^{l}|1\leq i\leq n\}\)，那么每次我们都需要重新计算\(W_K x_i^l和W_{V} x_{i}^{l}\)。所以，KVCache的想法也很简单，我们就不要保存\(x^l_i\)，直接保存\(W_K x_i^l和W_{V} x_{i}^{l}\)就可以，它们分别就是K cache 和 V cache。当然，其实还有别的cache选择，比如保存\(x^l_i\)。又或者根据矩阵乘法的性质：\(s_{i}=(W_{Q} x_{n+1}^{l})^{T}(W_{K} x_{i}^{l})=(x_{n+1}^{l})^{T}W_{Q}^{T}W_{K} x_{i}^{l}\)，也可以选择保存\(W_{Q}^{T}W_{K} x_{i}^{l}\)。

3、KVCache的存储及实现细节

KVCache的总大小为\(2ndLH=2nDL\)，正比于当前token数量、向量维度、层数。这里面最难处理的是token数量n，这是一个在推理过程中不断变大的量。具体处理方法有三种：

• 分配一个最大容量的缓冲区。要求提前预知最大的token数量，但是大部分的用户请求都很短。因此，按照最大容量来分配是非常浪费的。
• 动态分配缓冲区大小。超过容量了就扩增一倍，但是频繁申请、释放内存的开销很大，效率不高。
• 把数据拆散，按最小单元存储，用一份元数据记录每一块数据的位置。

最后一种方案，就是目前采用最多的方案，也叫PageAttention。程序在初始化时申请一整块显存，按照KVCache的大小划分成一个一个的小块，并记录每个token在推理时要用到第几个小块。小块显存的申请、释放、管理，类似操作系统对物理内存的虚拟化过程，这就是大名鼎鼎的vLLM的思路。

4、KVCache成立条件

KVCache是一种用更大的显存空间换取更快的推理速度的手段。那么，它是否能够无条件适用于所有的LLM呢？其实并不是的。分析了它的原理后，可以得出它适用的条件：如果把一层transformer层的计算效果记为\(f\)，那么它是一个接受变长输入的函数，输出也是变长的：\((x_1^{l+1},\cdots,x_i^{l+1},\cdots,x_n^{l+1})=f(x_1^l,\cdots,x_i^l,\cdots,x_n^l)\)​。举个例子，当增加m个token进行推理时： \[ (\hat{x}_{1}^{l+1},\cdots,\hat{x}_{i}^{l+1},\cdots,\hat{x}_{n}^{l+1},\hat{x}_{n+1}^{l+1},\cdots,\hat{x}_{n+j}^{l+1},\cdots,\hat{x}_{n+m}^{l+1})\\=f(x_1^l,\cdots,x_i^l,\cdots,x_n^l,x_{n+1}^l,\cdots,x_{n+j}^l,\cdots,x_{n+m}^l) \] 要适用KVCache，新的推理结果必须满足\(\hat{x}_{i}^{l+1}=x_{i}^{l+1},1\leq i\leq n\)。通俗来说，这一个性质可以称为“因果性”，每一个token的输出只依赖于它自己以及之前的输入，与之后的输入无关。在transformer类模型中，BERT类encoder模型不满足这一性质，而GPT类的decoder模型因为使用了causal mask，所以满足这一性质。但是这一方法并不是适用于全部的decoder-only模型，像一些ReRope之类的技术，在增加新的token时会把整个序列的positional embedding进行调整，同一个token，上一次的token embedding和这一次的token embedding不相同，所以KVCache的条件不再成立。而一旦输入预处理层不满足KVCache的条件，后续transformer层的输入（即预处理层的输出）就发生了改变，也将不再适用于KVCache。